分治算法
分治算法练习
求最大值
题目描述
给定一个有 $n$ 个数的序列,请用分治法求得最大值,输出其最大值。
输入格式
第一行为一个整数 $n$,第二行 $n$ 个整数 $a_i$。
输出格式
输出最大值。
输入样例
6
3 10 8 20 12 9输出样例
20数据范围
$1\le n\le 100,\ a_i \le 10^9$
试题分析
试题分析原问题是下标
[1, n]的序列里找最大值通过
mid分成左右两个子问题:子问题1:在
[L, mid]的序列里找最大值子问题2:在
[mid+1, R]的序列里找最大值
求解:如果子序列长度只有 1 :
L >= R,返回a[R]如果只使用
L>R,调用f(L, mid)在L==R的时候会死循环
合并:
max(子问题1的解,子问题2的解)
参考代码
参考代码:::details 分治使用
#include<iostream>
using namespace std;
#define N 100
int a[N],n;
int f(int l, int r){
if(l>=r) return a[r];
//分
int mid, ma1, ma2;
mid = (l + r) / 2;
ma1 = f(l, mid);
ma2 = f(mid + 1, r);
//治
if(ma1 > ma2)
return ma1;
else
return ma2;
}
int main(){
cin >> n;
for(int i = 1; i <= n; i++)
cin >> a[i];
cout << f(1,n);
return 0;
}:::
时间复杂度分析
只有一个数的时候不用比较,两个数的时候:
$T(2)=1$
有 $n$ 个数的时候:
$\begin{aligned}\T(n) &= 2T(n/2) + 2 \\&= 2[2T(n/4) + 2] + 2 = 2^2T(n/4) + 2^2 + 2 \\&= 2^2[2T(n/8) + 2] + 2^2 + 2 = 2^3T(n/8) + 2^3 + 2^2 + 2 \\&\dots \\&= 2^{k-1}T(2) + 2^{k-1} + 2^{k-2} + \dots + 2 \\&= 2^{k-1} + 2^k-1 \\end{aligned}$
令 $n = 2^k$,因此有:
$T(n) = n/2 + n - 1 = 3n/2 - 1$
复杂度也为 $O(n)$,但比直接循环比较的 $2n-3$ 次要少。
最大值与最小值
题目描述
给定一个有 $n$ 个数的序列,请用分治法求出其最大值与最小值。
输入格式
第一行为一个整数 $n$,第二行 $n$ 个整数 $a_i$。
输出格式
输出最大值与最小值。
输入样例
8
10 9 8 5 35 13 2 14输出样例
35 2数据范围
$1\le n\le 100$
分析
分析1、分治的思路
使用两个函数 f1 和 f2,分别使用分治求出最大值和最小值。
2、函数同时返回最大值和最小值
return 只能返回一个值,如果想要同一个函数记录最大和最小值,可以使用全局变量,也可以使用引用参数 int &ma, int &mi。
参考答案
参考答案:::details 双函数
#include<iostream>
using namespace std;
#define N 100
#define inf 0x7fffffff
int a[N],n;
int max(int l, int r) {
if (l >= r) return a[r];
int mid, ma1, ma2;
mid = (l + r) >> 1;
ma1 = max(l, mid);
ma2 = max(mid + 1, r);
if(ma1 > ma2)
return ma1;
else
return ma2;
}
int min(int l, int r) {
if (l >= r) return a[r];
int mid, mi1, mi2;
mid = (l + r) >> 1;
mi1 = min(l, mid);
mi2 = min(mid + 1, r);
if (mi1 < mi2)
return mi1;
else
return mi2;
}
int main() {
int mi, ma;
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
//输出
cout << max(1, n) << ' ' << min(1, n);
return 0;
}:::
:::details 引用传递
#include<bits/stdc++.h>
using namespace std;
#define N 100
#define inf 0x7fffffff
int a[N], n;
void mami(int l, int r, int &ma, int &mi) {
//边界
if (l >= r) {
ma = a[r];
mi = a[r];
return;
}
//分
int mid, lmi = inf, lma = 0, rmi = inf, rma = 0;
mid = (l + r) >> 1;
mami(l, mid, lma, lmi);
mami(mid + 1, r, rma, rmi);
//治理
ma = max(lma, rma);
mi = min(lmi, rmi);
return;
}
int main() {
int mi, ma;
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
//函数调用
mami(1, n, ma, mi);
//输出
cout << ma << ' ' << mi;
return 0;
}
:::
归并排序
归并排序(Merge-sort)是利用分治(divide-and-conquer)策略实现的排序方法,该算法采用经典的。
将大数组的排序问题分(divide)成小数组的排序问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的有序子序列按顺序合并在一起,即分而治之。
1.1 算法描述
归并排序分的过程是通过递归函数,将序列每次尽量对半分,直到只剩一个数(一个数视为有序)为止。
治的过程则是合并,将两个小的有序部分合并为大的有序部分。
1.2 图示

归并排序核心代码
void mergeSort(int L, int R) {
//边界
if(L >= R) return;
//分
int mid = (L+R) / 2;
mergeSort(L, mid);
mergeSort(mid + 1, R);
//治(合并数组)
merge(L, mid, R);
}1.3 具体的合并过程图示


核心代码
void merge(int L, int mid, int R) {
int i = L, j = mid+1, k = L;
while(i <= mid && j <= R) { //两个数组合并,直到一个数组为空
if(a[i] <= a[j]) {
temp[k++] = a[i];
i++;
} else {
temp[k++] = a[j];
j++;
}
}
while(i <= mid) { //前一个数组没处理完,全部加到临时数组
temp[k++] = a[i];
i++;
}
while(j <= R) { //后一个数组没处理完,全部加到临时数组
temp[k++] = a[j];
j++;
}
//将临时数组放回原数组
for(int i = L; i <= R; i++) {
a[i] = temp[i];
}
}逆序对问题
设 $A$ 为一个有 $n$ 个数字的有序集 $(n>1)$,如果存在正整数 $i$、$j$ 使得 $1 ≤ i < j ≤ n$ 而且 $A[i] > A[j]$,则 $<A[i], A[j]>$ 这个有序对称为 $A$ 的一个逆序对,也称作逆序数,可在归并排序的合并过程中顺便求出。
void merge(int L, int mid, int R) {
int i = L, j = mid+1, k = L;
while(i <= mid && j <= R) {
if(a[i] <= a[j]) {
temp[k++] = a[i];
i++;
} else {
temp[k++] = a[j];
ans += mid-i+1; //a[i] > a[j],a[i]后面的都大于 a[j],因此个数为 mid - i + 1
j++;
}
}
while(i <= mid) {
temp[k++] = a[i];
i++;
}
while(j <= R) {
temp[k++] = a[j];
j++;
}
for(int i = L; i <= R; i++) {
a[i] = temp[i];
}
}演示-归并排序-合并方法
一、背景
一、背景归并排序是分治法应用的一个完美例子,将序列递归分成两个子序列直到排序完成,然后将两个排好序的子序列合并成一个完整序列。
归并排序的核心是合并,将两个排好序的子序列合并成一个序列。
例如:
4 5 7 8 与 1 2 3 6
合并成:
1 2 3 4 5 6 7 8二、实验目标
二、实验目标编写merge函数,将数组a的两个递增子序列[L, mid]与(mid, R]合并起来,替换掉a里面的值,使得a序列为递增序列。
void merge(int L, int mid, int R) {
} 测试数据-代码里写死:
a[N] = {0, 4, 5, 7, 8, 1, 2, 3, 6};//L=1, mid=4, R=8输出-输出合并好的数组:
1 2 3 4 5 6 7 8数据范围:a序列长度不超过100
二、分析
二、分析1、合并思路
a[]的两个子序列[1, 4]与[5, 8]都为递增子序列,将他们合并起来。
用i指向子序列a1的下标(初始为1),用j指向子序列a2的下标(初始为5)。
方法:持续比较a[i]与a[j]的大小,小的值放到temp数组里去,然后小的下标加1。
最后将temp数组拷贝回a数组。
2、模拟过程
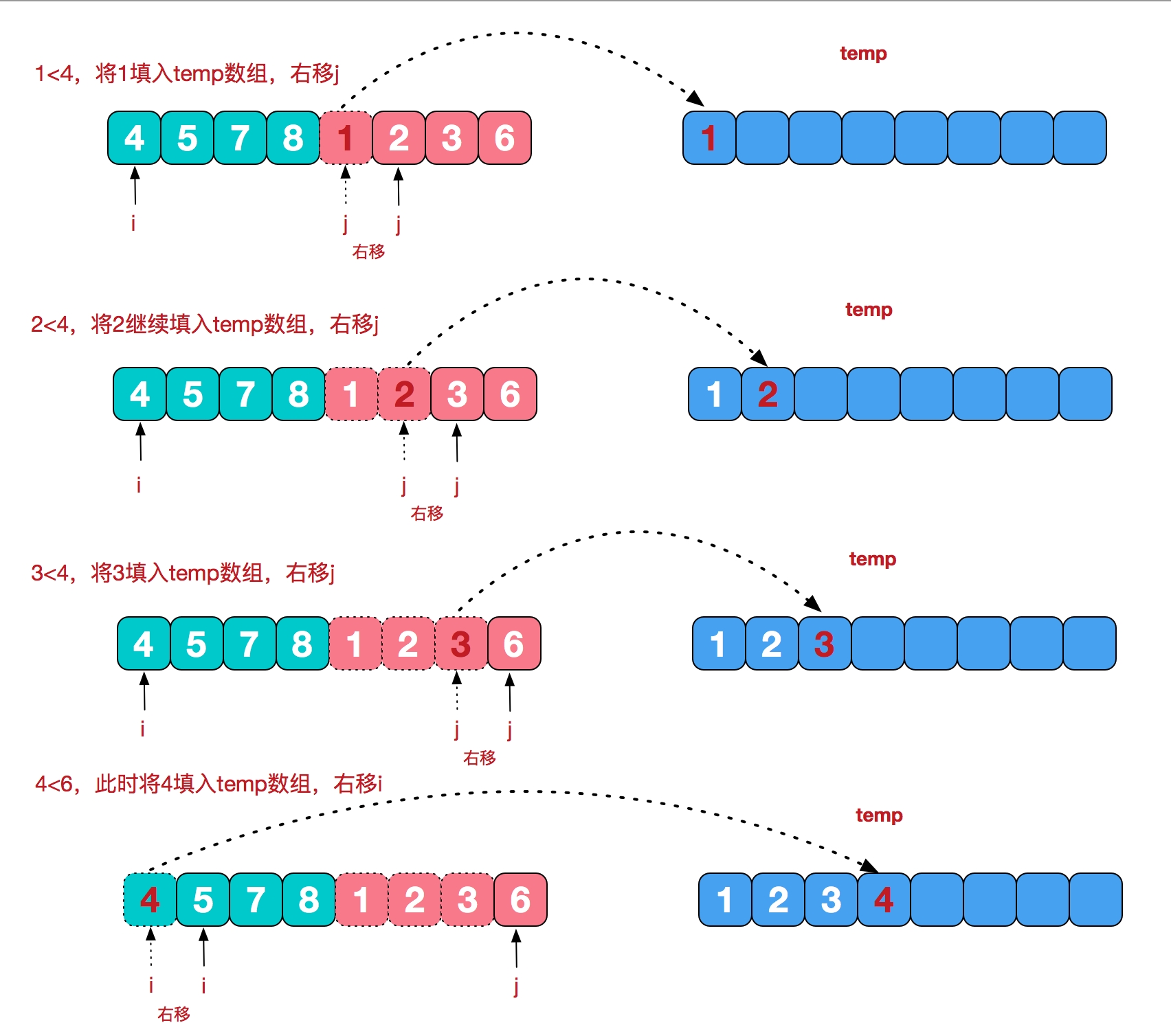
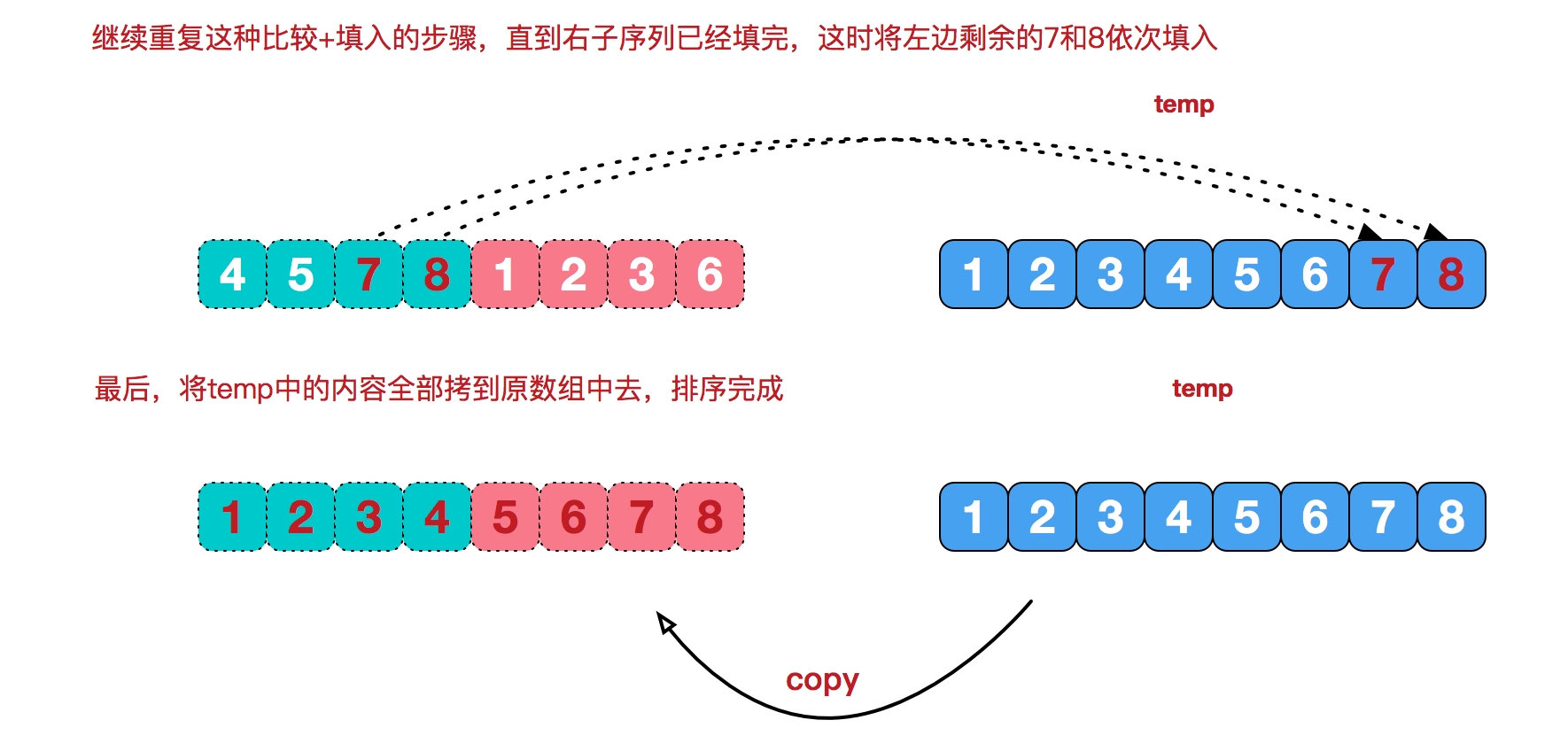
3、算法描述
参考以上图片:
第一步:循环两个下标,每次使得最小的值都存储到temp数组去,直到某一个子序列取光。
第二步:将另一个子序列剩余的也放到temp数组取。
第三步:拷贝回原数组(注意a数组要移位:L+i)。
三、实验步骤
三、实验步骤请自己实现:
数据定义
merge函数
main里调用与输出
#include <iostream>
using namespace std;
const int N= 101;
int a[N] = {0, 4, 5, 7, 8, 1, 2, 3, 6};
int temp[N];
void merge(int L, int mid, int R) {
int i=L, j=mid+1, k=L;
while(i<=mid && j<=R) {
if(a[i]<=a[j]) {
temp[k++] = a[i];
i++;
} else {
temp[k++] = a[j];
j++;
}
}
while(i<=mid) {
temp[k++] = a[i];
i++;
}
while(j<=R) {
temp[k++] = a[j];
j++;
}
for(int i=L; i<=R; i++)
a[i] = temp[i];
}
int main() {
merge(1, 4, 8);
for(int i=1; i<=8; i++)
cout<<a[i]<<" ";
return 0;
}演示-归并排序
一、实验目标
一、实验目标实现归并排序的算法实现递增排序,并在main里输入一个1..n的序列进行测试。
输入样例-第一行n,第二行n个元素:
8
8 4 5 7 1 3 6 2输出样例-排好序(递增)的数组:
1 2 3 4 5 6 7 8二、思路
二、思路1、归并排序思路
首先考虑当数组只有一个元素时,自然就是排序的数组。
其次,当两个数组(各一个元素),可以将其合并成一个数组。
依次类推,当两个n/2已排好序的子序列,可以将其合并成一个有序序列。
因此,利用分治的思想:
将数组每次二分成两个子序列
分别求解(排序完成的子序列)
合并
2、merge函数
参照上一题-合并。
3、mergeSort函数
如果L>=R就返回
计算mid,递归调用[L, mid]和(mid, R)
调用merge进行合并
三、实验步骤
三、实验步骤数据定义与输入
merge函数,可测试
mergeSort函数
main里调用和输出
#include<iostream>
using namespace std;
const int N= 101;
int n, a[N];
int temp[N];
void merge(int L, int mid, int R) {
int i=L, j=mid+1, k=L;
while(i<=mid && j<=R) {
if(a[i]<=a[j]) {
temp[k++] = a[i];
i++;
} else {
temp[k++] = a[j];
j++;
}
}
while(i<=mid) {
temp[k++] = a[i];
i++;
}
while(j<=R) {
temp[k++] = a[j];
j++;
}
for(int i=L; i<=R; i++)
a[i] = temp[i];
}
void mergeSort(int L, int R) {
if(L >= R) return;
int mid = (L+R)/2;
mergeSort(L, mid);
mergeSort(mid+1, R);
merge(L, mid, R);
}
int main() {
cin>>n;
for(int i=1; i<=n; i++)
cin>>a[i];
mergeSort(1, n);
for(int i=1; i<=n; i++)
cout<<a[i]<<" ";
return 0;
}演示-逆序对(归并排序)
题目描述
题目描述求逆序对个数
逆序对 设 A 为一个有 n 个数字的有序集 (n>1),其中所有数字各不相同。如果存在正整数 i, j 使得 1 ≤ i < j ≤ n 而且 A[i] > A[j],则 <A[i], A[j]> 这个有序对称为 A 的一个逆序对,也称作逆序数。比如数组(3,1,4,5,2)的逆序对有(3,1),(3,2),(4,2),(5,2),共4个。
输入输出格式
输入输出格式输入格式:
第一行 一个数n,表示序列中有n个数。
第二行 n个数,表示给定的序列。序列中每个数字不超过10^12
输出格式:
给定序列中逆序对的数目。
输入输出样例
输入输出样例输入样例:
6
5 4 2 6 3 1输出样例:
11测试点
测试点测试点:5个测试点,每个测试点得20分。
测试限制:每个测试点时间限制1s,内存限制128M。
数据范围:
20%:n≤100
60%:n≤4×10^4
100%:n<=5x10^5
1<=所有数据<=5x10^5
分析
分析1、朴素算法
复杂度o(n^2),大概能得20分,双重循环即可。
2、归并排序
比如将下面两个区间排序
a_i mid=4 a_j
左3,4,7,9 右1,5,8,10
首先将右区间的 1 取出,放到r_k中,此时 1 是比每个a_i中的元素都小,也就是说此时i的指针指向a_1的位置,此刻得到的逆序对的数量为 4; r_k= 1
然后再将a_i和a_j比较(直到a_i<a_j),a_i<a_j,将a_i的元素放到r_k中; r_k= 1,3,4;
现在a_j>a_i, i 指向a_3的位置,将 5 放到r_k中,得到的逆序对数量为 2 ; r_k= 1,3,4,5
以此类推,直到进行完归并排序,每次合并都会求出逆序对的数目,即mid-i+1,最后每次将ans加上mid-i+1即可得到最后的答案。
细节:被谁淘汰到tr_k时,就根据对方位置来计算。
/*#include<iostream>
using namespace std;
const int maxn=999999999;
const int minn=-999999999;
long long b[500005];//暂时存储用
long long n,a[500005],ans;
void my_sort(int left,int right) {
int mid=(left+right)/2;
if(left>=right) {
return ;
}
my_sort(left,mid);
my_sort(mid+1,right);
int i=left,j=mid+1,n=mid,m=right,k=0;
while(i<=n&&j<=m)
if(a[i]>a[j]) {
ans+=n-i+1;
b[k++]=a[j++];
} else
b[k++]=a[i++];
while(i<=n)
b[k++]=a[i++];
while(j<=m)
b[k++]=a[j++];
for(i=0; i<k; i++)
a[left+i]=b[i];
}
int main() {
cin>>n;
for(int i=1; i<=n; ++i) {
cin>>a[i];
}
my_sort(1,n);
cout<<ans;
return 0;
}*/
#include<iostream>
using namespace std;
const int N= 1e6;
long long n, a[N], temp[N],ans=0;
void merge(long long L, long long mid, long long R) {
long long i=L, j=mid+1, k=L;
while(i<=mid && j<=R) {
if(a[i]<=a[j]) {
temp[k++] = a[i];
i++;
} else {
temp[k++] = a[j];
ans += mid-i+1;//a[i] > a[j],a[i]后面的都>a[j],因此个数为mid - i + 1
j++;
}
}
while(i<=mid) {
temp[k++] = a[i];
i++;
}
while(j<=R) {
temp[k++] = a[j];
j++;
}
for(long long i=L; i<=R; i++)
a[i] = temp[i];
}
void mergeSort(long long L, long long R) {
if(L >= R) return;
long long mid = (L+R)/2;
mergeSort(L, mid);
mergeSort(mid+1, R);
merge(L, mid, R);
}
int main() {
cin>>n;
for(long long i=1; i<=n; i++)
cin>>a[i];
mergeSort(1, n);
cout<<ans<<endl;
return 0;
}
/*//暴力40来分
#include <iostream>
#include <cstdio>
using namespace std;
const int N= 5*1e5+5;
int n, a[N], temp[N],ans;
int main() {
cin>>n;
for(int i=1; i<=n; i++)
scanf("%d", &a[i]);
for(int i=1; i<=n ;i++)
for(int j=i+1; j<=n; j++)
ans += a[i]>a[j];
cout<<ans<<endl;
return 0;
}
*/